Hubungan Antara 2 Sudut

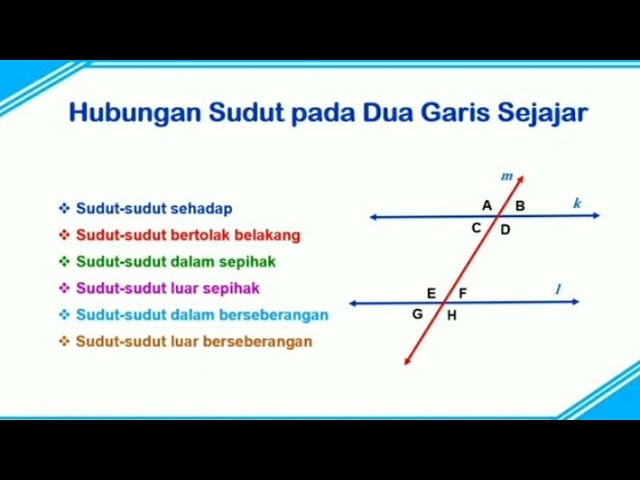
Pada kesempatan kali ini kita juga akan membahas tentang hubungan antar sudut. Hanya saja pembahasan kali ini kita akan berfokus mengenai bagaimana hubungan antar sudut apabila sudut-sudut tersebut sehadap, bersilangan, luar sepihak maupun dalam sepihak.

Selain itu, kita juga akan sedikit belajar contoh soal beserta pembahasanya, supaya sobat sekalian lebih mudah memahami materi kali ini.

Untuk lebih jelasnya, yuk simak…

Sudut – Sudut Sehadap

Coba perhatikanlah gambar berikut ini:

Pada gambar diatas, garis A dan B sejajar (A // B) dan dipotong oleh garis C. Titik potong yang diciptakan oleh garis C terhadap garis A dan B, secara berurutan pada gambar diatas nampak jika sudut D1 dan sudut E1 menghadap ke arah yang sama, begitu juga dengan sudut D2 dan E2, kemudian sudut D3 dan sudut E3, dan juga pada sudut D4 dan sudut E4.

Nah sudut-sudut yang menghadap kearah yang sama tersebut dinamakan dengan sudut sudut sehadap. Besarnya sudut yang sehadap adalah sama.

Jadi, jika ada dua buah garis yang sejajar, yang kemudian terpotong oleh garis yang lain, maka akan menghasilkan empat pasang sudut sehadap yang besar sudutnya sama. Jika Dituliskan yakni:

∠D1 sehadap dengan ∠E1 , sehingga besarnya sudut ∠D1 = ∠E1

∠D2 sehadap dengan ∠E2 , sehingga besarnya sudut ∠D2 = ∠E2

∠D3 sehadap dengan ∠E3 , sehingga besarnya sudut ∠D3 = ∠E3

∠D4 sehadap dengan ∠E4 , sehingga besarnya sudut ∠D4 = ∠E4

Contoh Soal nya:

Perhatikanlah gambar berikut:

a). Sebutkanlah pasangan sudut sudut yang sehadap.

b).Jika ∠N2 = 78°, tentukanlah besarnya ∠N1, ∠M1, dan ∠M2

Penyelesaian:

a). Menurut gambar pada soal maka diperoleh:

∠M1 sehadap dengan ∠N1

∠M2 sehadap dengan ∠N2

∠M3 sehadap dengan ∠N3

∠M4 sehadap dengan ∠N4

b). Jika ∠N2 = 78°, maka

∠N1 + ∠N2 = 180 ° (Berpelurus), sehingga

∠N1 + 78° = 180 ° ,

∠N1= 180 ° – 78° ,

∠N1= 102 °

∠M1 = ∠N1 (Sehadap)

∠M1 = 102 °

∠M2 = ∠N2 (Sehadap)

∠M2 = 78 °

Lanjut ke materi…

Sudut – Sudut Bersebrangan

Perhatikanlah gambar berikut:

Pada gambar diatas, ∠D3 letaknya bersebrangan dalam dengan ∠E1, kemudian ∠D4 bersebrangan dalam dengan ∠E2. Pasangan kedua sudut ini, disebut dengan sudut-sudut dalam bersebrangan, dan besarnya sudut yang bersebrangan dalam adalah sama besar. kemudian,..

Pada gambar diatas, ∠D1 letaknya bersebrangan luar dengan ∠E3, kemudian ∠D2 bersebrangan luar dengan ∠E4. Pasangan kedua sudut ini, disebut dengan sudut-sudut luar bersebrangan, dan besarnya sudut yang bersebrangan luar adalah sama besar.

Contoh Soalnya:

Perhatikan gambar berikut:

a). Sebutkanlah pasangan sudut – sudut dalam yang bersebrangan

b). Jika ∠M2 = 123° , tentukanlah besarnya ∠M1, ∠M3, dan ∠N4.

Penyelesaian:

q). Pada gambar diperoleh:

∠M1 Bersebrangan dalam dengan ∠N3

∠M2 Bersebrangan dalam dengan ∠N4

b). Jika ∠M2 = 123° maka;

∠M1 + ∠M2 = 180° (Berpelurus)

∠M1 + 123° = 180°

∠M1= 180° – 123°

∠M1 = 57°

∠M3 = ∠M1 (Bertolak Belakang)

∠M3 = 57°

∠N4 = ∠M2 (Dalam Bersebrangan)

∠N4 = 123°

Lanjut Ke..

Sudut-sudut Dalam Sepihak

Perhatikanlah Gambar Berikut:

Pada gambar diatas, garis A dan garis B letaknya sejajar (A // B). Kedua garis tersebut dipotong oleh garis C pada titik D dan E. Jika diperhatikan pada titik perpotongannya didapati bahwa ∠D3 dan ∠E2, letaknya berada di dalam garis, dan sepihak disebelah kanan. Begitu juga dengan ∠D4 dan ∠E1 yang juga terletak sepihak disebelah kiri. Pasangan sudut yang seperti ini dikenal dengan nama Sudut-sudut dalam sepihak. Sehingga dapat ditulis dengan:

• ∠D3 sepihak dengan ∠E2 dan
• ∠D4 sepihak dengan ∠E1

Pada pembahasan sebelumnya, kita telah mengenal bahwa:

∠D3 = ∠E3 (sehadap), dan

∠D2 = ∠E2 (sehadap)

padahal ∠D2 = 180° – ∠D3, sehingga

∠E2 = ∠D2 = 180° – ∠D3 atau ∠D3 + ∠E2 = 180°

Jadi perpotongan dari dua garis yang sejajar akan menghasilkan jumlah sudut-sudut dalam sepihak sebesar 180°, dan dengan cara yang sama kita juga bisa membuktikan bahwa ∠D4 + ∠E1 = 180°

Contoh Soalnya:

Pada gambar diatas, garis A dan B letaknya sejajar (A // B). Kedua garis tersebut dipotong oleh garis U pada titik S dan T.

a). Tentukanlah pasangan sudut-sudut dalam sepihak

b). Jika ∠T4 = 95°, tentukanlah ∠S3 dan ∠S2.

Penyelesaian:

a). Menurut gambar pada soal, maka diperoleh:

∠S3 dalam sepihak dengan ∠T4, dan

∠S2 dalam sepihak dengan ∠T1.

b). Jika ∠T4 = 95°, maka

∠S3 + ∠T4 = 180 ° (dalam sepihak)

∠S3 + 95° = 180 °

∠S3 = 180 ° – 95°

∠S3 = 85°

∠S2 = ∠T4 = 95° (dalam bersebrangan)

Sudut-sudut Luar Sepihak

Perhatikanlah gambar berikut:

Jika diperhatikan, pada gambar diatas ∠D1 dengan ∠E4 dan ∠D2 dengan ∠E3. Pasangan sudut tersebut disebut dengan sudut-sudut luar sepihak. Kita akan membuktikan bahwa ∠D1 + ∠E4 = 180°.

∠D1 + ∠D4 = 180° (berpelurus)

padahal ∠D4 = ∠E4 (sehadap), sehingga terbukti bahwa

∠D1 + ∠E4 = 180°

Jadi kesimpulannya yaitu jika dua garis sejajar dipotong oleh garis yang lain maka jumlah sudut-sudut luar sepihaknya yaitu sebesat 180°

Demikianlah sobat, materi mengenai “Hubungan Sudut – Sudut Sehadap,Bersebrangan, Dalam Sepihak, dan Luar Sepihak”

Sedikit yang dapat kami sampaikan. Semoga bermanfaat, dan sampai jumpa pada kesempatan yang lain

Sumber: rumushitung.com